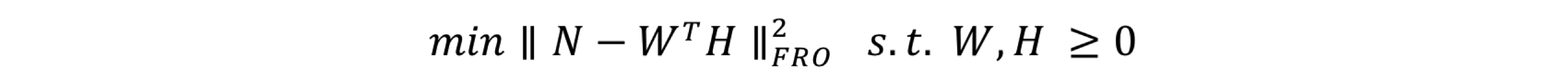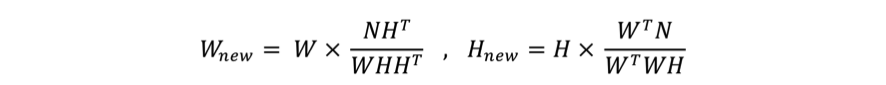Twitterのホームタイムラインを取得して, 顔認識とツイートを定期的に実行する仕組みをサーバーレス環境 (GCP) に実装しました.
(意訳：推しの画像をリツイートしてみんなに見てもらいたかった@pedigree_C)

推しの方々からいいねをもらったりもらわなかったり, 評判がなかなか良いです(?)

全体のソースコードと詳細は https://github.com/camberbridge/dft-gcp-serverless にありますのでよろしければご覧ください.

アーキテクチャ

何と言っても特筆すべきは Cloud Functions の柔軟さです.

関数が何らかの原因でクラッシュしても, 「失敗時に再試行」の設定をしておけば最大7日間 (2021年現在), 関数が正常に完了するまで繰り返し呼び出されます (タイムアウト時間は設定可能).

また, リクエストの多さによってインスタンス数が自動でスケールします. もちろんこの時の上限数は設定可能です.
今回は, 毎分の小さな定期実行なのでスケーリングしなくても間に合うだろうと思っていましたが, 画像付きツイートが多いと (顔認識があるので) 関数の処理に時間がかかって次のリクエスト処理に間に合わないことが多々ありました.

そんなときに Cloud Functions は自動でスケールアウトして, 逆に画像付きツイートが少ないとスケールインしてくれて, 非常に便利でした.

サーバーレス環境 (GCP)

DBにCloud Datastore

Twitterのホームタイムラインを定期的に取得する際, 前回取得したTweet IDよりも新しいものだけを取得するようにしたかったので, 最新のTweet IDを保持しておく必要がありました.
そこで, (DBを用意するまでもない構成ですが) 環境をステートレスにしたかったこともあり, ドキュメントDBの Cloud Datastore を用いました$^1$.

Tweet IDを書き込むときはデータを増やす理由がないので同じエンティティを更新し続けるようにしました.
ベストプラクティス的には, 「1つのエンティティをあまり頻繁に (1秒に1回以上) 更新しないこと」とありますが, ここでは毎分の更新なので良しとします$^2$.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

from google.cloud import datastore

datastore_client = datastore.Client()
# エンティティの種類
kind = "Twitter_home"
# エンティティの名前/ID
name = "latest_tweet_id"
entity_key = datastore_client.key(kind, name)

def put_latest_tweet_id(tweet_id):
    entity = datastore.Entity(key=entity_key)
    entity["id"] = tweet_id

    # エンティティ保存
    datastore_client.put(entity)

def get_latest_tweet_id():
    # エンティティ取得
    entity = datastore_client.get(key=entity_key)

    return entity["id"]

※ローカル環境から Datastore にアクセスする (上のコードを実行する) 場合はサービスアカウントを発行する必要があります$^3$

プログラムの実行環境にCloud Functions

イベント単位の実行に適したサーバーレスコンピューティングリソースの Cloud Functions を用いました.
基本的にはGCPコンソールで作成と設定が可能ですが, 顔認識に必要なOpenCVのDNNモデル等のファイルをコンソールからアップロードできません.

そこで, ソースコードやアセットをzip化したファイルを gsutil で Cloud Storage にアップロードしておき, その後の gcloud による Functions デプロイ時に, オブジェクトURLを指定してあげます$^4$.

1
2
3
4
5
6
7
8
9
10
11
12

$ zip -r [FILE_NAME].zip *
$ gsutil mb -p [GCP_PROJECT_ID] -l US-CENTRAL1 gs://[BUCKET_NAME]
$ gsutil cp [FILE_NAME].zip gs://[BUCKET_NAME]
$ gcloud functions deploy [FUNCTION_NAME] \
  --source=gs://[BUCKET_NAME]/[FILE_NAME].zip \
  --stage-bucket=[BUCKET_NAME] \
  --trigger-topic=[Pub/Sub_TOPIC_NAME] \
  --memory=256MB \
  --runtime=python37 \
  --region=us-central1 \
  --project=[GCP_PROJECT_ID] \
  --entry-point=main

定期実行のトリガーにCloud Scheduler x Pub/Sub

cronと同じ要領で使える Cloud Scheduler から毎分 Pub/Sub トピックをパブリッシュして Cloud Functions をトリガーさせました.
トピックは gcloud コマンドでデプロイする時に作成 (Pub/Sub_TOPIC_NAME の部分) しており, 受けの Functions にも設定しているので, あとは出す側の Cloud Scheduler の設定をします.
やり方は, GCPコンソールでリージョンやcron, トピックを指定するだけです$^5$.

その他

デプロイ時やプログラム実行時の成功/失敗など, ログ監視に Cloud Logging が大変役に立ちます.
また, エラー確認には, Cloud Error Reporting がすごく便利です. Twitter APIにレート制限があることをすっかり忘れていて, 実際に Error Reporting からメールが届いたおかげで気づけました (後述の wait_on_rate_limit を設定したきっかけ).

Twitter API (Tweepy)

レート制限の対処

無料アカウントの場合, ホームタイムライン取得リクエストの制限回数は15分に15回 (2021年現在) です$^6$.
結構シビアですが, Tweepyにはレート制限が補充されるのを自動的に待つ (エラーハンドリングせずに放置できる！) 便利なパラメータ wait_on_rate_limit があるのでそれを使います$^7$.

1
2
3
4
5

import tweepy

auth = tweepy.OAuthHandler(CONSUMER_KEY, CONSUMER_SECRET)
auth.set_access_token(ACCESS_TOKEN, ACCESS_TOKEN_SECRET)
api = tweepy.API(auth, wait_on_rate_limit=True)

ホームタイムライン取得

今回の仕組みは定期実行させるので, 毎度同じツイートを取得する可能性があります.
そこで, これまた便利なパラメータ since_id を使い, あるIDよりも新しいツイートを取得するようにします.$^7$

1

timeline = api.home_timeline(since_id=TWEET_ID, count=N)

ツイート前処理とMedia URLの取得

推しが投稿するツイートだけを取得したいので, 前処理として”RT @”を含むツイートを除外します.
ちなみにただのリツイートはホームタイムライン取得のレスポンスには入ってきません.

1
2
3
4
5
6
7

for status in timeline:
    # リツイートを除外
    if not "RT @" in status.text[0:4]:
        if "media" in status.entities:
            for media in status.extended_entities["media"]:
                # Media URL取得
                media_url = media["media_url"]

引用リツイート

元ツイートのURLをTweet本文に貼るだけで引用リツイートになります.
そしてアプリでリツイートした時と同様に, きちんと引用されたユーザに通知されます.

顔認識 (OpenCV DNN)

Web画像の読み込み

OpenCVでいろいろと画像処理をするため, Media URLから画像を一時ファイルとしてダウンロードしました.
このとき画像は /tmp ディレクトリに保存することがポイントです.
これは, Cloud Functions のファイルシステムで書き込み可能な場所 (一時ファイルの保存先として使用できる場所) は /tmp ディレクトリだけとなっているからです$^8$.

そして画像ファイルをOpenCVで読み込み, 処理の高速化のためあらかじめサイズを半分にしておきました.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

import numpy as np
import cv2
import tempfile
import requests

def imread_web(url, flags=cv2.IMREAD_COLOR, dtype=np.uint8):
    try:
        res = requests.get(url)
        # URLをダウンロードして一時ファイルとして保存
        with tempfile.NamedTemporaryFile(dir="/tmp/") as fp:
            fp.write(res.content)
            fp.file.seek(0)

            n = np.fromfile(fp.name, dtype)
            img = cv2.imdecode(n, flags)
            img_h, img_w = img.shape[:2]
            img_hf_w = img_w // 2
            img_hf_h = img_h // 2
            halfimg = cv2.resize(img, (img_hf_w, img_hf_h))
            return halfimg
    except Exception as e:
        return None

OpenCV DNNに入力する画像を正方形にリサイズ

画像をOpenCV DNNに入力する前に, 画像を正方形にリサイズしておく必要があります.
OpenCV DNNの顔認識では最初にBlobオブジェクトを blobFromImage() で作るのですが, このときの処理が同じ幅と高さの画像を要するからです$^9$.

1
2
3

img_size = 600
blob = cv2.dnn.blobFromImage(cv2.resize(img, (img_size, img_size)), 1.0,
                             (img_size, img_size), (104.0, 177.0, 123.0))

顔認識の実行

検出結果それぞれには信頼度があるので, それをよしなに使います.
いろいろと試行錯誤した結果, 0.9よりも大きければ顔と判定することにしました. 今のところ仕組みは顔写真付きツイートだけに反応できているのでいい感じです.

# 事前学習済み DNN caffe model
# 参考: https://github.com/spmallick/learnopencv/tree/master/FaceDetectionComparison/models
PROTOTXT_PATH = "./deploy.prototxt"
WEIGHTS_PATH = "./res10_300x300_ssd_iter_140000_fp16.caffemodel"
# 信頼度閾値
CONFIDENCE = 0.9
face_num = 0

# モデルのロード
net = cv2.dnn.readNetFromCaffe(PROTOTXT_PATH, WEIGHTS_PATH)
net.setInput(blob)
detections = net.forward()

for i in range(0, detections.shape[2]):
    confidence = detections[0, 0, i, 2]
    # 顔検出
    if confidence > CONFIDENCE:
        face_num += 1

参考文献

[1] “Datastore mode Client Libraries”. https://cloud.google.com/datastore/docs/reference/libraries

[2] “ベストプラクティス - エンティティの更新”. https://cloud.google.com/datastore/docs/best-practices#updates_to_an_entity

[3] “Datastore mode Client Libraries - Setting up authenticaiton”. https://cloud.google.com/datastore/docs/reference/libraries#setting_up_authentication

[4] “Google Cloud Pub/Sub トリガー - 関数のデプロイ”. https://cloud.google.com/functions/docs/calling/pubsub#deploying_your_function

[5] “Pub/Sub を使用して Cloud ファンクションをトリガーする - Cloud Schedulerジョブを作成する”. https://cloud.google.com/scheduler/docs/tut-pub-sub#create_a_job

[6] “Get Tweet timelines - Resource Information”. https://developer.twitter.com/en/docs/twitter-api/v1/tweets/timelines/api-reference/get-statuses-home_timeline

[7] “Tweepy API Reference”. https://docs.tweepy.org/en/latest/api.html

[8] “Cloud Functions 実行環境 - ファイルシステム”. https://cloud.google.com/functions/docs/concepts/exec#file_system

[9] “OpenCV Deep Neural Network module”. https://docs.opencv.org/master/d6/d0f/group__dnn.html

概要

Jaccard係数は集合間の類似度を表す尺度(値域は0から1の間)であり, (1)式により定義されます(値が1に近づくほど類似度が高い).

$sim(C_i, C_j) = \frac{\mid C_i \cap C_j \mid}{\mid C_i \cup C_j \mid}$ ・・・(1)

一般に, (1)式はDBの中からクエリqとのJaccard係数が大きいデータ(集合)を探すような場合に, データ数nやデータの要素数dが大きいと計算時間($O(nd)$)が非常に大きくなる問題があります${}^{※1}$.
そこで今回は, 集合に対する確率的なハッシュ関数であるMin Hashを用いて, Jaccard係数を近似計算する実験を行ってみます. Min HashはJaccard係数に対するLocality Sensitive Hashingです.
※1 扱うデータはそれぞれ要素の種類数を次元とした2値ベクトル表現に変換しているとします.

Jaccard係数の性質

2つのベクトル$C_i = (1, 1, 0, 0)$, $C_j = (1, 0, 1, 0)$があるとします.

このとき各列は値によって4種類に分類でき, タイプDはJaccard係数に関係ないので, $C_i$, $C_j$間の類似度は(2)式で表現できます.

$sim(C_i, C_j) = \frac{\mid A \mid}{\mid A \mid + \mid B \mid + \mid C \mid}$　・・・(2)

Min Hashの性質

Min Hashは, ベクトルの列入れ替え規則を持ったハッシュ関数mhをそれぞれのベクトルに適用した後, 最初に非ゼロが出現する位置(ハッシュ値)が一致する確率によってJaccard係数を近似する手法です. したがって, ベクトルの列をランダムに入れ替えたときにタイプA, B, Cのどれが最初に出現するかでハッシュ値が一致するかどうかが決まるため, 結局タイプDは関係なく, (3)式で表現されます.

$P[mh(C_i) = mh(C_j)] = \frac{\mid A \mid}{\mid A \mid + \mid B \mid + \mid C \mid}$　・・・(3)

なお, 実際にMin Hashを使うときはベクトルの列を入れ替えることはせずにランダムに生成したハッシュテーブル$r_{(t)}$を用意し, ハッシュテーブルを通してハッシュ値を求めます(データベースで列の入れ替えは処理が重いため).

例：$r_{(t)} = $ {$6, 1, 2, 3, 8, 7, 5, 4$}, $C_i = (1, 0, 0, 0, 1, 1, 1, 0)$のとき, $mh(C_i) = min${$6, 8, 7, 5$} $ = 5$

つまりMin Hashは作成したハッシュ関数(ハッシュテーブル$r_{(t)}$)をそれぞれの集合に適用した後に最小値を求め, それが一致する確率でJaccard係数を近似します. ハッシュ値が一致する確率は経験確率により近似計算します. 具体的には,

1. k個のハッシュ関数を用意し, $C_i$, $C_j$に対するk個のハッシュ値${}^{※2}$を得る
2. $C_i$, $C_j$のk個のハッシュ値のうち, いくつが一致するか数える
3. 一致した数をkで割った確率がJaccard係数の近似値となる

kの数を増やせば増やすほど, 近似値はJaccard係数に近づきます.
※2 k個のハッシュ値はsketchとも呼ばれます.

重要な定理

ここで重要な定理は, $C_i$, $C_j$のハッシュ値が一致する確率はJaccard係数と等しいということです.

$P[mh(C_i) = mh(C_j)] = \frac{\mid C_i \cap C_j \mid}{\mid C_i \cup C_j \mid} = sim(C_i, C_j)$　・・・(4)

方針

• DBの中からクエリの類似データを検索するタスクを用意します
• Jaccard係数とMin Hashによる近似Jaccard係数を用いて類似データを検索します
• Jaccard係数での検索結果を正解データとして, 近似Jaccard係数での検索結果でPrecision Recall Curveを作成します
• kを増やすほどJaccard係数による検索結果に近づくのか, カーブの下がり具合を見て確かめます(カーブの右肩が座標(1, 1)に近いほど, Min Hashによる近似値はJaccard係数に近い)

方法

1. 150個の集合をランダムに生成する
   • 集合の要素種類数を400とし, 各要素を含むかどうかは確率的に決定する
2. 集合の20%をクエリ, 80%をDBとする
3. クエリとのJaccard係数が大きい上位20個の集合を正解データとする
4. 近似Jaccard係数による検索結果の上位100個について, Precision Recall Curveを作成する(ハッシュ値の数k = 100, 1000, 10000の場合について)
   • $Precision = \frac{近似Jaccard係数による検索結果上位x個のうち正解データに入っているものの数}{検索結果件数x}$
   • $Recall = \frac{近似Jaccard係数による検索結果上位x個のうち正解データに入っているものの数}{正解データ数}$
   • 変数$x$は1~100

実装

Jaccard係数とMin Hashの実装

1. Jaccard係数とMin Hashを実装します. すべての集合を2値ベクトル表現にし, プログラムの実行時に引数でsketchの数kを指定できるようにしました.

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105

   # -*- coding: utf-8 -*- from abc import ABCMeta, abstractmethod import random import sys import math class SimilarityCal(object): __metaclass__ = ABCMeta @abstractmethod def calculate(self, set_x, set_y): raise NotImplementedError("not implemented error.") # 重複要素のない集合の生成 def uniqueSet(self, set_x, set_y): x = set(list(set_x)) y = set(list(set_y)) return x, y # 2値ベクトルの生成 def binaryVector(self, set_x, set_y): # 集合の要素種類数 set_xy = set(list(set_x)) | set(list(set_y)) x = [] y = [] for v in set_xy: if v in set_x: x.append(1) else: x.append(0) if v in set_y: y.append(1) else: y.append(0) return x, y # 1~引数lengthの範囲で重複なしの乱数を引数length分生成 (length = 集合の要素種類数) def generateRanNum(self, length): samples = random.sample(xrange(length + 1), length + 1) r_t = [] for v in samples: if v != 0 and len(r_t) < length: r_t.append(v) return r_t # Jaccard係数 class Jaccard(SimilarityCal): def calculate(self, set_x, set_y): x, y = self.uniqueSet(set_x, set_y) try: # 積集合/和集合 result = float(len(x & y)) / len(x | y) except ZeroDivisionError: result = 0.0 return result # MinHash class MinHash(SimilarityCal): def calculate(self, set_x, set_y): bagOfX, bagOfY = self.binaryVector(set_x, set_y) # 生成するMinHashの数 k = int(sys.argv[1]) # k個のハッシュ値のうち, いくつ一致したか counter = 0 # 第一引数kの回数分ハッシュ関数を生成し, 比較する for i in xrange(k): hashX = [] hashY = [] # r(t)テーブルの生成 r_t = self.generateRanNum(len(bagOfX)) for i in xrange(len(bagOfX)): if bagOfX[i] == 1: hashX.append(r_t[i]) mh_x = min(hashX) for i in xrange(len(bagOfY)): if bagOfY[i] == 1: hashY.append(r_t[i]) mh_y = min(hashY) counter = counter + 1 if mh_x == mh_y else counter # MinHashを用いたJaccard係数の近似計算の結果を返す return float(counter) / k if __name__ == '__main__': set_x = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 111, 555, 31, 49, 100, 1000, 1111, 111] set_y = [2, 3, 4, 6, 11, 22, 33, 44, 55, 111, 1111, 1000, 100, 10] print "MinHash", MinHash().calculate(set_x, set_y) print "Jaccard", Jaccard().calculate(set_x, set_y)

2. それではハッシュ値の数k = 5で実行してみます. なお, まとめたコードはGitHubにあげています.

   1 2 3

   $ python jaccard_minhash.py 5 MinHash 0.2 Jaccard 0.409090909091

3. 次はk = 7で実行.

   1 2 3

   python jaccard_minhash.py 7 MinHash 0.571428571429 Jaccard 0.409090909091

4. k = 10で実行. kを増やすとMinHashによる近似Jaccard係数がJaccard係数に近づいていることが確認できます.

   1 2 3

   $ python jaccard_minhash.py 10 MinHash 0.4 Jaccard 0.409090909091

Precision Recall Curveを描画

1. データセットを生成します. 具体的には, 150個の集合をランダムに生成します. そして各集合の要素種類数を400とし, 各要素を含むかどうかは確率的に決定します. 用意したデータセットの20%をクエリ, 80%をDBとします.

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

   # sketchの個数 kNum = 100 # 集合の個数 n = 150 # n個の集合 sets = [] # 要素の値域を[1, 400]つまり要素の種類数dを400にする d = 400 # 集合の要素数を確率的に決める prob = 0.3 # n個の集合を生成 for i in xrange(n): ary = [v for v in xrange(1, d + 1) if random.random() < prob] sets.append(ary) # setsのうち20%をクエリ, 80%をDBにする pivot = int(math.ceil(len(sets)*0.2)) query = sets[:pivot] db = sets[pivot:]

2. Jaccard係数が大きい上位20個の集合を正解データとします.

   1 2 3 4 5 6 7 8 9 10 11 12 13 14

   # クエリとDBのJaccard係数を計算して値の昇順にソート aryJaccard = [] for set_x in query: for set_y in db: dictJaccard = {} dictJaccard["Set"] = set_y dictJaccard["Score"] = Jaccard().calculate(set_x, set_y) aryJaccard.append(dictJaccard) # 種類数 = query数 * db数 aryJaccard = sorted(aryJaccard, key = lambda x:x["Score"]) # Jaccard係数が大きい上位20件のDBを正解データとして使う if len(aryJaccard) > 20: aryJaccard = aryJaccard[-20:]

3. kを100, 1000, 10000と変化させたときのPrecision Recall Curveを描画します. なお, PrecisionはInterpolated Precisionにしています.

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64

   plotDataSets_x = [] plotDataSets_y = [] plotDataSets_label = [] while kNum <= 10000: aryMinHash = [] for set_x in query: for set_y in db: dictMinHash = {} dictMinHash["Set"] = set_y dictMinHash["Score"] = MinHash().calculate(set_x, set_y, kNum) aryMinHash.append(dictMinHash) # 種類数 = query数 * db数 aryMinHash = sorted(aryMinHash, key = lambda x:x["Score"]) # MinHashによる近似Jaccard係数が大きい上位x(1~100)件 plotData_x = [] plotData_y = [] for x in xrange(1, 101): MinHashResultStat = aryMinHash[-x:] # MinHashとJaccardの結果で一致する数をカウント counter = 0 for dict_M in MinHashResultStat: MinHashResult = set(dict_M["Set"]) countFlag = False for dict_J in aryJaccard: JaccardResult = set(dict_J["Set"]) if len(MinHashResult) == len(JaccardResult): counter = counter + 1 if len(MinHashResult & JaccardResult) == len(MinHashResult) else counter countFlag = True if countFlag: break if counter >= 20: break print x, ",", kNum, ",", counter, ",", (float(counter)/x), ",", (float(counter)/20) plotData_x.append(float(counter)/20) plotData_y.append(float(counter)/x) # interpolated precision for i in xrange(1, len(plotData_y)): if plotData_y[len(plotData_y)-i] > plotData_y[len(plotData_y)-(i+1)]: plotData_y[len(plotData_y)-(i+1)] = plotData_y[len(plotData_y)-i] plotDataSets_x.append(plotData_x) plotDataSets_y.append(plotData_y) plotDataSets_label.append("k="+str(kNum)) kNum *= 10 # グラフ生成 fig = sns.mpl.pyplot.figure() ax = fig.add_subplot(111) for i in xrange(len(plotDataSets_label)): ax.plot(plotDataSets_x[i], plotDataSets_y[i], label=plotDataSets_label[i]) ax.legend() sns.plt.title(u"Min HashによるJaccard係数の近似値を用いた類似検索結果のPrecision Recall Curve") sns.plt.xlabel(u"Recall") sns.plt.ylabel(u"Precision") sns.plt.show()

4. 実行結果です. まとめたコードはGitHubにあげています.
   

kを増やすほどカーブの右肩が座標(1, 1)に近づいていることが確認できます. 検索結果の精度が良くなっている(Min HashによるJaccard係数の近似値がJaccard係数に近づいている)ようです.

まとめ

本記事ではLocality Sensitive HashingであるMin Hashを用いて, Jaccard係数を近似する実験を行いました. 近似していることの確認は, Min Hashで生成するハッシュ値の数kを増やしていくことにより, 正解(Jaccard係数で導出したデータ)をどれだけ当てられるかを, Min Hashによる近似値についてのPredision Recall Curveを作成することで確かめました.

結果の図より, kを増やすとカーブの右肩が座標(1,1)に近づくため, Jaccard係数で導出した結果に近づいていくことを確認できました.

参考文献

• “Jaccard係数とMin Hash“.
• “Min Hashによる高速な類似検索“.

自己相互情報量とは, 2つの事象の間の関連度合いを測る尺度である(負から正までの値をとる).
自然言語処理では自己相互情報量が相互情報量と呼ばれることがある. しかし, 情報理論で定義される相互情報量(後述する)とは全く異なるため, 自己相互情報量と呼ぶのが賢明である.
自然言語処理に関する本や論文では略称のPMIがよく用いられる.

PMIの定義

確率変数のある実現値xと, 別の確率変数のある実現値yに対して, 自己相互情報量PMI(x, y)は,

$PMI(x, y) = \log_2\frac{P(x, y)}{P(x)P(y)}$ ・・・(1)

と定義され, 値が大きければ大きいほどxとyの関連している度合いが強い.

• PMIが正の値の場合
  • $P(x, y) > P(x)P(y)$ ⇒ $PMI(x, y) > 0$
  • xとyが一緒に出現しやすい. (独立よりも)共起しやすい傾向にある.
• PMIが負の場合
  • $P(x, y) < P(x)P(y)$ ⇒ $PMI(x, y) < 0$
  • xとyが一緒に出現しにくい. (独立よりも)共起しにくい傾向にある.
• PMIが0の場合
  • $P(x, y) = P(x)P(y)$ ⇒ $PMI(x, y) = log1 = 0$
  • xとyの関連がない. それぞれ独立に出現する.
• 正の値, 負の値の絶対値が大きいほど傾向が強い.

相互情報量 (Mutual Information, MI) について

• MIとは, PMIの平均(確率変数X, Yの全ての実現値$x_{i}$, $y_{i}$に関して平均をとったもの)である.
• PMIは実現値(スカラー)の対に関して定義される量に対し, MIは確率変数(ベクトル)の対に関して定義される量である.

MIの定義

2つの確率変数XとYに対し, 相互情報量MI(X, Y)は,

$MI(X, Y) = \sum_{x, y} P(x, y)\log_2\frac{P(x, y)}{P(x)P(y)}$ ・・・(2)

と定義され, 0以上の値をとる $^1$.

自然言語処理におけるPMI

PMIの値が示す2つの事象の関連度合いは, 自然言語処理においては単語の共起性と捉えることができ, さらに単語の意味的な類似性と近似できる(2つの単語が一緒に起こりやすい場合は, 意味的にも関連しているだろうという直感に基づいて).
ここでxとyを単語とすると,

• ある文中でx, yがそれぞれ出現する確率は$P(x)$, $P(y)$
• x, yが文中に同時に出現する確率は$P(x, y)$

と表される.
式は以下の通り.

$PMI(x, y) = \log_2\frac{P(x, y)}{P(x)P(y)} = \log_2\frac{\frac{C(x, y)}{N}}{\frac{C(x)}{N} \cdot \frac{C(y)}{N}} = \log_2\frac{C(x, y) \cdot N}{C(x)C(y)}$ ・・・(3)

単語の出現確率について

単語の出現確率は, 最尤推定で決定されることが多い $^2$.
各単語の出現確率が二項分布に従っているとし, 尤度から最尤推定によって単語の出現確率の式を導出している例はこちら

PMIの式の意味

(1)式を変形すると, 以下のようになる.

$PMI(x, y) = \log_2\frac{P(x, y)}{P(x)P(y)} = \log_2\frac{P(x \cap y)}{P(x)P(y)} = \log_2\frac{P(x)P(y \vert x)}{P(x)P(y)} = \log_2\frac{P(y \vert x)}{P(y)} = \log_2{P(y \vert x)} - \log_2{P(y)}$ ・・・(4)

(4)式は, 単語xが出現したときに単語yが出現する確率について, y単体での出現確率を引いたものである.
つまりPMIの式は, “単語の共起確率から単語単体での出現確率の影響を差し引くことで, より正確に単語間の共起を測ろうとしている”と理解できる.
例えば, “the”のようにどの文中にも現れるような単語は, 他のどの単語に対しても共起確率$P(“the”, w)$が高くなるので, 結果としてPMIの値が大きくなり, 関連が高いと判断されてしまう.
これを防ぐために”the”単体での出現確率を差し引くことで, 他単語との関連度を低くできる.

PMIの使い方

単語総数が10000の文書内にある2つの単語”自然”と”言語”の関連度を測るとする.
文中に”自然”が120回, “言語”が40回出現し, 20回共起しているとすると(3)式より,

$PMI(自然, 言語) = \log_{2}\frac{20 \cdot 10000}{120 \cdot 40} \approx 5.38$

共起の判定方法

2つの単語が共起関係にあるかどうかの判定方法は, 単語Bigramや単語10-gramを使い, 単語xの前後2単語以内もしくは10単語以内に単語yが出現するかどうかで判定することがある $^3$$^,$$^4$.
つまり, 単語の共起確率は単語n-gramでの共起を基に求めるということ.

PMIの抱える問題と解決策

PMIには2つの問題があるため, 使う際には考慮する必要がある.

1. 共起頻度が0の場合, PMIが計算できない問題

単語の共起頻度が0の場合,

$P(x,y) = 0$ ⇒ $PMI(x, y) = -∞$

と発散してしまい, PMIが計算できない問題がある.

解決策

この問題に対し, 共起頻度が0の時点でPMIの値を0とするか, もしくはPMI導出式の共起確率部分に一定のパラメータを加算するスムージング(平滑化)がよく行われる $^5$$^,$$^6$.

• 共起頻度が0の時点でPMIの値を0にする
  • これは単純であるが, 負の値をとるPMIの値を0に丸め込んでしまうため, 「xとyが共起しにくい特徴」を無くしてしまう問題がある.
• スムージング
  • 慣例として対数をとる際に共起頻度に1が加算される.
    • 1を加算することによるPMIへの影響については, 一定のパラメータを加えたところでPMI同士を比較したときの順序関係は変わらないため, 問題ない.
  • その都度手動でパラメータを調整する場合もある $^7$.
    • 参考文献[7]では, 以下の計算式によってスムージングを行っている.
      • $N’(x, y) = N(x, y) + C$ ・・・(5)
      • $P_{smooth} (x, y) = \frac{N’(x, y) + αP(x)P(y)}{1 + α}$ ・・・(6)
    • パラメータC, αはクロスバリデーションによって最適値を決め, そのパラメータを使ったスムージング共起確率$P_{smooth} (x, y)$を使ってPMIを計算している.

2. 出現頻度の低い単語同士が共起した場合にPMIの値が非常に大きくなる問題

例として単語総数が10000の文書について, 以下の2つの場合を考える.

• C(x, y) = 1, C(x) = 1, C(y) = 1の場合
  • PMI(x, y) = log(10000)
• C(x, y) = 1000, C(x) = 1000, C(y) = 1000 の場合
  • PMI(x, y) = log(10)

単語xとyがそれぞれ1000回出現していて, さらにそれが常に共起している2つ目のPMIの方が値は大きいはずだが, 1つ目の単語の出現頻度が低い場合のPMIの方が大きい.
この問題は単語の出現確率が最尤推定による推定量であることが関係しており, 最尤推定で求めた出現確率が単語の正確な出現確率と大きく異なっていることが原因であると考えられる.

解決策

この問題を解決するためには単語の出現確率をより正確に求めることが必要である.
したがって単語の出現確率に最尤推定量を使うのではなく, 事後分布最大化推定値(maximum a posterior estimator, MAP 推定値)などの他の推定手法を用いればよい.

参考文献

[1]　“例題：相互情報量の性質”.
　　http://omm.ishikawa-nct.ac.jp/ex/exercises/Pj0GgAAA/#answer

[2]　“単語の出現確率の最尤推定”
　　http://id.fnshr.info/2012/01/24/wordmle/

[3]　“FSNLP 5.4 Mutual Information(相互情報量)”
　　http://d.hatena.ne.jp/n_shuyo/20100827/fsnlp

[4]　鍋島啓太. “構成性に基づく評価極性知識獲得“. 2011.

[5]　岩成達哉ら. “多様な手がかりを用いた形容詞に基づく概念語の順序付け“. 2016.

[6]　仁科俊晴ら. “対義形容詞対との相互情報量を利用した概念語の順序付け“. 2013.

[7]　Gang Guoら. “A COMPARATIVE STUDY ON VARIOUS CONFIDENCE MEASURES IN LARGE VOCABULARY SPEECH RECOGNITION“. 2004.

[8] 高村大也. “言語処理のための機械学習入門”. 2011.

※ [8]については1.6章と4.6章を参考にした.

概要

スマホでGoogle検索エンジンを使ってWeb検索すると, 検索結果画面はスマホの画面サイズにアレンジされたものとなって表示される. さらに検索結果件数が表示されなくなったりと, 表示そのものの簡単化も行われる.

自分はFirefox add-on for mobileの開発で, WebIDF (Web Inverse Document Frequency) を特徴量のひとつとして使っている関係上, 検索結果件数を取得できないことは致命傷. そこでGoogle検索結果画面のPC版表示がどうしても必要だったので, その対処法を示す.

対処法

検索結果画面のURL末尾にパラメータ&nomo=1を付与する.

1

https://www.google.co.jp/search?q=<検索クエリ>&nomo=1

これによってPC版の検索結果画面が表示される. そして検索結果件数が欲しいなら好みのやり方で#resultStatsを指定して取得するだけ.

おまけ

Google検索結果画面の表示件数を変更したい場合にも上記方法は使える. Google検索エンジンの設定画面のURL末尾にパラメータ&nomo=1を付与してアクセスすれば詳細な設定変更を行うことができる.

概要

半年前から先輩の誘いでJava講習の非常勤講師を”ときどき”やっている. そしてその講習会の特に初心者向けでは, 意外な質問が飛んできたり受講者分のエラーコードが見られたりするので, 結構楽しい.
そこで今回は質問の中で「ああそういえば」となった事を書き残す. それはJavaで識別子にUnicode文字が使えるよって(まぁ言語仕様の)お話.

言語規定 - 識別子

Javaでは文字リテラルや文字列リテラル, 識別子(クラス, メソッド, 変数名)にUnicode文字を使うことができる. それらはUTF-8, UTF-16で書くもよし, エスケープ記法で書くもよし.
下記例は識別子をUTF-8で書いた場合のプログラムである. これをExample.javaとして保存し, コンパイルしてから実行すればちくわと最も相性のいい”きゅうり”を表示する!…はず!!

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

public class Example {
        static class ちくわについて {
                String これでしょ;

                void に合うものは (String 相性) {
                        これでしょ = 相性;
                }

                String に合うもの(){
                        return これでしょ;
                }
        }

        public static void main (String[] args){
                ちくわについて ちくわ = new ちくわについて();
                ちくわ.に合うものは("きゅうり");

                System.out.println(ちくわ.に合うもの());
        }
}

上記例で示したことはJavaの言語規定にしっかりと記されている(Java言語規定 - 3.8識別子).

おまけ

これを応用?した面白い例を紹介します.

1
2
3
4
5
6
7
8
9
10
11

\u0070\u0075\u0062\u006c\u0069\u0063\u0020\u0020\u0020\u0020
\u0063\u006c\u0061\u0073\u0073\u0020\u0055\u0067\u006c\u0079
\u007b\u0070\u0075\u0062\u006c\u0069\u0063\u0020\u0020\u0020
\u0020\u0020\u0020\u0020\u0073\u0074\u0061\u0074\u0069\u0063
\u0076\u006f\u0069\u0064\u0020\u006d\u0061\u0069\u006e\u0028
\u0053\u0074\u0072\u0069\u006e\u0067\u005b\u005d\u0020\u0020
\u0020\u0020\u0020\u0020\u0061\u0072\u0067\u0073\u0029\u007b
\u0053\u0079\u0073\u0074\u0065\u006d\u002e\u006f\u0075\u0074
\u002e\u0070\u0072\u0069\u006e\u0074\u006c\u006e\u0028\u0020
\u0022\u0048\u0065\u006c\u006c\u006f\u0020\u0077\u0022\u002b
\u0022\u006f\u0072\u006c\u0064\u0022\u0029\u003b\u007d\u007d

!?
!?!?
自分はUnicodeマスターではないため分かりませんでしたが, 実行すると”Hello world”と表示します. これはUgly.javaとして保存すればちゃんと扱えるプログラムなのです.
下記は実際にこれをマルチバイト文字に変換したものです.

1
2
3
4
5

public class Ugly {
        public static void main (String[] args) {
                System.out.println("Hello w" + "orld");
        }
}

ちなみに, このおまけはJava PuzzlersというJavaの問題集に載っています. 難しいけどオススメです.

環境

• OS X
• Python 2.7系
• TensorFlow 0.7系

概要

TensorFlowでRNNのPTB LSTM model(ptb_word_lm.py)の実行を試みたところ, エラーになったので, その対処をしました.
カレントディレクトリはptb_word_lm.pyがある階層です.

エラー1「AttributeError: ‘module’ object has no attribute ‘gfile’」

GitHubのissue #1121によると, ズバリ0.6.0を使ってくれとのことでした. よって今のところはブランチを0.6.0に変えて解決です(vrvさんによると現在バグ対処してくれている模様です).

エラー2「ImportError: No module named ptb」

ptb_word_lm.pyのfrom tensorflow.models.rnn.ptb import readerをimport readerにして解決です.

エラー3「TypeError: unsupported operand type(s) for /: ‘Tensor’ and ‘int’」

futureのdivisionモジュールでの割り算でエラーが出ています.
これはPython 3系を使っていれば起こらないエラーのようです. 自分は2.7系なのでfrom __future__ import divisionをコメントアウトして解決です.

エラー4「NameError: global name ‘time’ is not defined」

timeモジュールが見つからないためエラーが出ています.
import timeを追加して解決です.

概要

トピックモデルとは, 文書集合から特徴(話題)を抽出する手法です. また, それぞれの文書が持つ話題を抽出したり, 文書間の類似性を抽出することが可能な手法です.
そこで今回は, トピックモデルを用いてニュース記事を対象に話題を抽出する実験を行ってみます. なお, トピックモデルの中でも特に潜在意味解析(latent semantic analysis, LSA)を実際に用いています(正確には, LSAはベクトル空間モデルであり, このLSAを確率モデルに拡張した確率的潜在意味解析がトピックモデルです. しかし, トピックモデルのカテゴリ(離散値確率)分布は, LSAで用いる行列分解手法として捉えることができるので, 僕は同じ物として扱っています).

潜在意味解析(latent semantic analysis, LSA)

LSAは, 文書集合データを(文書総数 x 単語数)の行列Nで表現したときに, 掛け合わせることで再び元の行列を構築できるような, 小さな(低ランクの)2つの行列を見つけることをします(これを非負値行列因子分解と言います). このとき, それぞれの行列は特徴の組み合わせで構築されているため, この特徴を用いることによって文書に潜在するトピック(文書を特徴づける単語)を抽出します.

非負値行列因子分解(nonnegative matrix factorization, NMF)

NMFとは, 行列で表現した文字・画像・音声などのデータ(非負値行列)を指定する基底数に行列分解し, 低ランクの表現にすることによって, それぞれの行列が持つ潜在的な特徴を抽出することを可能にした行列低ランク近似手法です. 簡単に言えば, 非負値行列を2つの非負値行列に分解するアルゴリズムです. 以下, NMFについて詳細に説明します.

図1に示すように, 文書集合データを(D x V)の行列Nで表現するとします. ここでDは文書総数, Vは単語数です.

このNを分解すると, W(K x D)の基底行列とH(K x V)の特徴重みの行列となります. そしてこれらWとHを掛け合わせることにより, 元の行列Nの近似値が得られますが, 完全に一致する行列W, Hの値を求めるのは困難です.

そこで, この近似値を求める問題は, 行列Nと転置したWにHを掛け合わせた行列の距離を小さくする問題として扱うことができます. 具体的には, フロベニウスノルムの最小化を行います(図2).

フロベニウスノルムの最小化問題には, 模擬アニーリングや勾配降下法, 乗法的更新ルールなど, いくつかの数学的解法が提案されていますが, NMFで最も用いられる解法は乗法的更新ルールです(参考論文).
乗法的更新ルールの式を図3に示します.

そして, フロベニウスノルムの最小化問題を解くために, NMFでは行列WとHをランダムな値で初期化し, 乗法的更新ルールの式にしたがってWとHを更新して距離が収束するまでこの処理を繰り返します. NMFはこのようにして行列の低ランク近似を行います.

方針

• ニュース記事を文書として, 大量の文書から話題になっているトピックを抽出します. さらに, 話題になっているトピックを持つ文書を抽出します.
• 各文書が持つ潜在的な話題を抽出します.

方法

1. 様々な分野の情報を発信するサイトAll Aboutが公開しているRSSを用いて文書を収集する.
2. 収集した各文書について本文抽出, 形態素解析の処理を施すことによって形態素単位で分かち書きする.
3. 単語をBOW(bug-of-words)表現する.
   1. 各文書に存在する単語について, その文書における出現回数を数える.
   2. 全文書に存在する単語について, 全文書における出現回数を数える.
   3. 1と2から特徴行列と特徴単語の集合を生成する.
4. NMFを用いて文書の持つ潜在的な特徴を抽出する.

実装

BOWの実装

1. Pythonのfeedparserを用いてRSSから文書を取得します. この時, 出来るだけ異なる分野の記事(RSS)を取得するようにします. これはトピックモデル全般に言えることです. 今回は下記のRSSを使用しました.

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

   feedlist=['http://rss.allabout.co.jp/aa/latest/ch/health/', 'http://rss.allabout.co.jp/aa/latest/ch/house/', 'http://rss.allabout.co.jp/aa/latest/ch/domestic/', 'http://rss.allabout.co.jp/aa/latest/ch/ch_creditcard/', 'http://rss.allabout.co.jp/aa/latest/ch/beautydiet/', 'http://rss.allabout.co.jp/aa/latest/ch/mobile/', 'http://rss.allabout.co.jp/aa/latest/ch/pet/', 'http://rss.allabout.co.jp/aa/latest/ch/marriage/', 'http://rss.allabout.co.jp/aa/latest/ch/mensbeauty/', 'http://rss.allabout.co.jp/aa/latest/ch/fashion/', 'http://rss.allabout.co.jp/aa/latest/ch/ch_sweets/', 'http://rss.allabout.co.jp/aa/latest/ch/examination/', 'http://rss.allabout.co.jp/aa/latest/ch/auto/', 'http://rss.allabout.co.jp/aa/latest/ch/homeelectronics/', 'http://rss.allabout.co.jp/aa/latest/ch/ch_sports/', 'http://rss.allabout.co.jp/aa/latest/ch/ch_game/', 'http://rss.allabout.co.jp/aa/latest/ch/ch_hobby/']

2. 取得したHTMLから本文の抽出を行います. 具体的には, HTMLタグを除いた文字列を集める処理を施します.

   1 2 3 4 5 6 7 8 9 10

   def stripHTML(h): p='' s=0 for c in h: if c=='<': s=1 elif c=='>': s=0 p+=' ' elif s==0: p+=c return p

3. 抽出した本文を形態素単位で分かち書きします. 具体的には, 形態素解析器Janomeを用いて形態素解析し, 定める単語単位で分かち書きします. 定める単語は, 以下のルールに従う単語としました.
   • 名詞であること
   • 接尾辞でないこと
   • 代名詞でないこと
   • 非自立語でないこと
   • 数でないこと
   • 形容動詞語幹でないこと
   • (英単語の場合)文字列長が4以上であること
     下記, 単語を分割するコード.

     1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31

     def separatewords(text): separatedWord=[] t=Tokenizer() tokens=t.tokenize(unicode(text, "utf-8")) for token in tokens: posList=token.part_of_speech.split(",") pos1=posList[0] if isinstance(pos1, unicode): pos1=pos1.encode("utf-8") pos2=posList[1] if isinstance(pos2, unicode): pos2=pos2.encode("utf-8") ruby=token.reading if isinstance(ruby, unicode): ruby=ruby.encode("utf-8") if pos1=="名詞": if pos2!="接尾" and pos2!="代名詞" and pos2!="非自立" and pos2!="数" and pos2!="形容動詞語幹": if ruby!="*": separatedWord.append(token.surface.lower()) print token.surface.lower() elif pos2!="サ変接続" and len(token.surface)>3: # 英単語に関しては4文字以上の単語を扱う separatedWord.append(token.surface.lower()) print token.surface.lower() return separatedWord

4. 単語をBOW表現します. 具体的にはRSSで取得した文書について, タイトルと本文を抽出して存在する単語の数をカウントします. そして, 単語の出現回数を保持した行列を生成します.

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

   def getarticlewords(): allwords={} # 全文書の総単語とその出現回数 articlewords=[] # 各文書の総単語とその出現回数 articletitles=[] # 文書タイトル ec=0 for feed in feedlist: f=feedparser.parse(feed) # すべての記事をループする for e in f.entries: # 同一の記事の場合は飛ばす if e.title in articletitles: continue # 単語を抽出する txt=e.title.encode('utf8')+stripHTML(e.description.encode('utf8')) words=separatewords(txt) articlewords.append({}) articletitles.append(e.title) # allwordsとarticlewordsにあるこの単語のカウントを増やす for word in words: allwords.setdefault(word,0) allwords[word]+=1 articlewords[ec].setdefault(word,0) articlewords[ec][word]+=1 ec+=1 return allwords,articlewords,articletitles

5. 行を文書総数, 列を特徴単語総数とした特徴行列と, 全文書に存在する特徴単語の集合を生成します. なお, 特徴単語は一般的な単語であるが一般的すぎない単語としました. 具体的には, 1文書に出現する回数が4以上, かつ文書総数の6割未満の単語を特徴単語としました.

   1 2 3 4 5 6 7 8 9 10 11

   def makematrix(allw,articlew): wordvec=[] # 一般的だが一般的すぎない(特徴があるとする)単語のみを利用する for w,c in allw.items(): if c>3 and c<len(articlew)*0.6: wordvec.append(w) # 各文書における特徴単語の出現回数の分布を持つ行列(特徴行列)を生成する l1=[[(word in f and f[word] or 0) for word in wordvec] for f in articlew] return l1,wordvec

6. Pythonインタプリタを使い, 上記コードによって取得した文書から特徴単語を抽出し, BOW表現する様子を確認してみたいと思います. なお, 上記コードをまとめたファイルをGitHubにあげておきます.

   1 2 3 4 5 6 7 8 9 10 11 12

   $ python >>> import newsfeatures >>> allw,artw,artt=newsfeatures.getarticlewords() >>> wordmatrix,wordvec=newsfeatures.makematrix(allw,artw) >>> len(artt) 340 >>> len(wordvec) 513 >>> len(wordmatrix) 340 >>> len(wordmatrix[0]) 513

   取得した記事340個から特徴単語を513個抽出できました. そしてBOW表現した特徴行列wordmatrixが得られました.

NMFの実装

特徴行列が得られたので, NMFによって文書の持つ潜在的な特徴を抽出します.

1. フロベニウスノルムの最小化のために, 残差平方和を求めるプログラムを用意します.

   1 2 3 4 5 6 7

   def difcost(a,b): dif=0 for i in range(shape(a)[0]): # 行 for j in range(shape(a)[1]): # 列 dif+=pow(a[i,j]-b[i,j],2) return dif

2. NMFを実装します. 引数にはNMFする(numpyでmatrix化した)特徴行列, 因子の数, 乗法的更新ルールで更新する回数を与えます. なお, ここで与える因子の数が全文書から抽出したいトピックの数になります.

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32

   def factorize(v,pc=10,iter=50): ic=shape(v)[0] # vの行数 fc=shape(v)[1] # vの列数 # 重みの行列(w)と特徴の行列(h)をランダムな値で初期化 w=matrix([[random.random() for j in range(pc)] for i in range(ic)]) h=matrix([[random.random() for i in range(fc)] for i in range(pc)]) # 乗法的更新ルール. iter回繰り返す for i in range(iter): wh=w*h # 残差平方和の計算 cost=difcost(v,wh) # 10回ごとに残差平方和を表示 if i%10==0: print cost # 行列が完全に因子分解されたら終了 if cost==0: break # 特徴重みの行列を更新 hn=(transpose(w)*v) hd=(transpose(w)*w*h) h=matrix(array(h)*array(hn)/array(hd)) # 基底行列を更新 wn=(v*transpose(h)) wd=(w*h*transpose(h)) ## 実行時にエラー(RuntimeWarning: invalid value encountered in divide)が出るなら #wd = [[1e-20 if (x - 1e-20 < 0) else x for x in lst] for lst in wd.tolist()] w=matrix(array(w)*array(wn)/array(wd)) return w,h

3. 上記コードによって生成されるのは基底行列と特徴重みの行列なので, 抽出したトピックを見やすい形式で表示する&ファイルに書き出すプログラムを用意します.
   このプログラムにより, 抽出したトピック(トピックにおいて出現確率が高い特徴単語6個)と, そのトピックを持つ文書上位3件を表示&書き出します.

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44

   def showfeatures(w,h,titles,wordvec,out='features.txt'): with open(out, "w") as outfile: pc,wc=shape(h) toppatterns=[[] for i in range(len(titles))] patternnames=[] # 因子数分繰り返し for i in range(pc): slist=[] # 単語とその重みのリストを作る for j in range(wc): slist.append((h[i,j],wordvec[j])) # 単語のリストを降順に並び替え slist.sort() slist.reverse() # 上位6つの要素(特徴語)を出力 n=[s[1] for s in slist[0:6]] outfile.write(str(n)+'\n') print "トピック" + str(i+1) + ": ", for hoge in n: print hoge, print "" patternnames.append(n) # 当該特徴を持つ文書のリストを作る flist=[] for j in range(len(titles)): # 該当する重みに対応する文書タイトルを重みに結合 flist.append((w[j,i],titles[j])) toppatterns[j].append((w[j,i],i,titles[j])) flist.sort() flist.reverse() # 上位3つの文書を表示 for f in flist[0:3]: outfile.write(str(f)+'\n') for hoge in f: print hoge, print "" outfile.write('\n') return toppatterns,patternnames

4. 実際に, 特徴行列にNMFを適用して得られるトピックを確認してみます. なお, 因子数を20個, イテレーション数を50回としました.

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89

   >>> import nmf >>> v=matrix(wordmatrix) >>> weights,feat=nmf.factorize(v,pc=20,iter=50) 4644026.99428 6276.23883311 6106.81822625 6076.58094169 6064.71184922 >>> topp,pn=nmf.showfeatures(weights,feat,artt,wordvec) トピック1: メーカー 特徴 家 大手 マリオ 住宅 15.4663497597 ヒーターのメーカー別の特徴 13.3104830612 ゲーム業界から見たスーパーマリオメーカー問題 13.2819191304 似て非なる大手住宅メーカー10社の特徴まとめ【2016年版】 トピック2: ポイント 楽天 現金 方法 ネット スーパー 19.7595240853 無印良品で楽天スーパーポイントやTポイントを貯める 16.7933330305 ポイント交換手数料がかからずに現金化する方法とは？ 13.6775064617 Amazonの買い物で2つのポイントを貯める！ トピック3: カード ドコモ 利用 クレジットカード サービス メイン 22.0895104043 dポイントカードは持っていたほうが良い？ 17.0282753695 クレジットカード、2枚目はこうやって選べ！ 14.0005808073 まだまだあるdカード・dカード GOLDの魅力とは？ トピック4: 人 口内 口 トラブル 環境 悪化 23.2705036456 口臭や口内炎、原因は口内環境の悪化？ケアして解消 20.316718056 全身の健康は口から　口臭を「クマ笹歯みがき」で予防 6.55166834564 頭皮のかゆみ…くりかえす原因は常在菌による炎症？ トピック5: 紹介 方法 iphone 機能 今回 ダイエット 11.9575251978 iPhoneで着信時に通知ランプを点滅させる方法 10.3358206124 機能豊富なiPhoneのカメラアプリを使いこなそう 10.1530091745 iPhone標準ブラウザ「Safari」の便利機能10選 トピック6: 対策 指輪 雪 女性 試験 男性 15.9903054461 都心で雪が降る日に慌てないようやっておくべき全対策 12.2442409343 既婚者なのに結婚指輪をつけない男性のホンネと対策 8.33584814286 便秘太りさん必見、原因別の「腸活」便秘対策法 トピック7: 将棋 愛 ガイド 登場 宴会 シーン 19.9652514536 将棋ファン感涙！将棋シーンが登場する漫画10選 14.6345881045 愛棋家ぶらり旅ガイド(1)別府・将棋処「と」 14.2962735508 愛棋家のための宴会ソング-将棋替え歌・キュート編 トピック8: 子ども 薬 親 問題 ストレス 受験 19.6893953432 子どもの将来を受験で潰さないために…親の心得と接し方 17.960475885 アイスやジュースはNG！薬を嫌がる子供への飲ませ方 15.0014403268 子どもを薬嫌いにさせないための「服薬補助ゼリー」 トピック9: ヨガ ポーズ 人 犬 効果 下 24.9219551555 基本のヨガポーズをマスター！下を向いた犬のポーズ 15.0087767171 まずはココから！自宅でできる初心者向けのヨガポーズ 11.0473594218 初心者でも簡単!?「空中ヨガ」で新感覚エクササイズ トピック10: 体 幹 トレーニング メニュー 基本 効果 34.4317754799 体幹トレーニングの基本5メニューで、劇的に体型を変える！ 14.7631212143 冬太り撃退に！体幹トレーニング「レッグバランス」 13.7327354842 【動画】1分で簡単！効果絶大な体幹トレーニング3選 トピック11: 人気 パン カフェ コーヒー 栃木 中古 13.7362428489 栃木を訪れたら絶対食べたい！ 地元で愛される人気パン6選 12.6581465276 【中古車】ルパンにも登場した人気の名車6選【自動車】 10.5455508799 人気のフィアット500が新車時の半額以下に！ トピック12: 紹介 今回 日本 月 金沢 五輪 11.911419134 ルーペで味わい尽くす！凹版切手の魅力 11.4798284003 贈って喜ばれる！金沢っ子おすすめの新おいしいお土産 11.0113306297 これぞ日本の美！奥の細道シリーズの魅力に迫る！ トピック13: チョコ バレンタイン 褒美 自分 ショコラ チョコレート 22.566436019 スリーエフのバレンタイン2016！ご褒美チョコ＆感謝チョコ厳選5 19.0753834192 ファミマのバレンタイン2016！あの人気店の味＆本格チョコ厳選7 17.9912005562 自分へのご褒美チョコレート2016厳選バレンタイン トピック14: プレート ホット 鍋 グリル 方式 選び方 19.1341121925 ホットプレートとグリル鍋の違い 18.6032897757 ホットプレート・グリル鍋のメーカー別特徴 14.5889482845 ホットプレート・グリル鍋の加熱方式 トピック15: 木 魅力 街 プロ 紹介 場所 37.0109893407 街に暮らしにもっと木を！木のプロが語る「木化」とは 4.33374555819 自然豊かな表情が魅力の「国産ナラ材」 2.98959349923 プロは楽して踊っていると言う事実 トピック16: 住宅 建築 設計 事務所 経験 現在 21.6811595627 納谷学+納谷新［納谷建築設計事務所］ 16.2771733003 岸本和彦［acaa建築研究所］ 14.5906325228 ヴィンテージ住宅のリノベーション［井の頭の住宅］ トピック17: 猫 目 映画 今回 理由 妊娠 19.7927332553 猫の目を見つめてはダメ？ 18.6993266635 猫が帰って来ない!?迷い猫の探し方 16.6343533117 立つ猫――猫が二本足になる理由って？ トピック18: 塾 選び 受験 チェックポイント 中学生 失敗 24.2675675159 塾選び、個別指導塾の盲点とチェックポイント 21.8312760412 失敗しない塾選び、7つのポイント 14.4755082856 意外な盲点に注意！中学生の塾選びのポイント トピック19: 冬 雪見 露天風呂 温泉 紹介 季節 23.088694487 冬の温泉旅におすすめ！関東周辺の雪見露天風呂10選 17.645473759 脱・冬太り！スッキリボディを手に入れる冬太りストップダイエット 13.3875534695 美肌効果も期待大！ 東京から行ける雪見露天5選 トピック20: トレンド 春 夏 ファッション 厳選 キーワード 16.0910792269 2016春夏トレンド5「ランジェリーエッセンス」 14.6996582741 2016春夏トレンド6「モダンオールディーズ」 14.5019972252 2016春夏トレンド4「リーンエフォートレス」

   指定した因子数20個分のトピックと, それを最も表現する特徴単語(そのトピックにおいて出現確率が高い単語 = 共起する単語), およびそのトピックを持つ文書を1トピックにつき上位3件表示しました. なお, プログラムと同階層に結果を書き出したファイルfeatures.txtが生成されます.

結果を見ると, それぞれのトピック(各トピックにおいて出現確率が最も高い単語)ごとに関連した単語が抽出できていることが確認できます. 特にトピック13の「チョコ」なんかは, 「バレンタイン 褒美 自分 ショコラ チョコレート」のように, チョコととても関係の深い単語が抽出できていることがわかります.

さらに, そのトピックを持つ上位3件の文書を実際に確認したところ, トピック13のチョコにおいては, 「スリーエフのバレンタイン2016！ご褒美チョコ＆感謝チョコ厳選5 」「ファミマのバレンタイン2016！あの人気店の味＆本格チョコ厳選7 」「自分へのご褒美チョコレート2016厳選バレンタイン」の全てが, まさにチョコな記事でした.

最後に, 各文書が持つ潜在的なトピックを確認します. 下記コードでは, 各文書に潜在するトピックの上位3つを表示するとともに, 結果をファイルに書き出します.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

def showarticles(titles,toppatterns,patternnames,out='article.txt'):
    with open(out,'w') as outfile:

        # 全文書について
        for j in range(len(titles)):
            outfile.write(titles[j].encode('utf8')+'\n')
            print "-----" + str(j+1) + "-----" + "\n" + titles[j] + "\n"

            # この文書の特徴たちを取得しソートする
            toppatterns[j].sort()
            toppatterns[j].reverse()

            # 上位3トピックを出力する
            for i in range(3):
                outfile.write(str(toppatterns[j][i][0])+' '+str(patternnames[toppatterns[j][i][1]])+'\n')
                print "トピック" + str(i+1) + ": ",
                for hoge in patternnames[toppatterns[j][i][1]]:
                    print hoge,
                print ""

            outfile.write('\n')

それでは実行してみます.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148

>>> nmf.showarticles(artt,topp,pn)
-----1-----
肝臓疾患に効果を持つ唯一のロングセラー市販薬

トピック1:  子ども 薬 親 問題 ストレス 受験 
トピック2:  対策 指輪 雪 女性 試験 男性 
トピック3:  チョコ バレンタイン 褒美 自分 ショコラ チョコレート 
-----2-----
二日酔い対策の隠れたベストセラー市販薬「五苓散」

トピック1:  対策 指輪 雪 女性 試験 男性 
トピック2:  住宅 建築 設計 事務所 経験 現在 
トピック3:  人 口内 口 トラブル 環境 悪化 
-----3-----
頭皮のかゆみ…くりかえす原因は常在菌による炎症？

トピック1:  人 口内 口 トラブル 環境 悪化 
トピック2:  住宅 建築 設計 事務所 経験 現在 
トピック3:  子ども 薬 親 問題 ストレス 受験 
-----4-----
赤ちゃんから大人まで骨の健康に不可欠なビタミンD

トピック1:  紹介 方法 iphone 機能 今回 ダイエット 
トピック2:  紹介 今回 日本 月 金沢 五輪 
トピック3:  子ども 薬 親 問題 ストレス 受験 
-----5-----
飲みにくい薬は「ゼリーの力」で解決を！

トピック1:  子ども 薬 親 問題 ストレス 受験 
トピック2:  紹介 方法 iphone 機能 今回 ダイエット 
トピック3:  ヨガ ポーズ 人 犬 効果 下 
-----6-----
大事なプレゼン前に「声」が出ない、さあどうする？

トピック1:  紹介 方法 iphone 機能 今回 ダイエット 
トピック2:  木 魅力 街 プロ 紹介 場所 
トピック3:  猫 目 映画 今回 理由 妊娠 
-----7-----
すっきりしない胃の不調は「健胃」と「制酸」で治す！

トピック1:  トレンド 春 夏 ファッション 厳選 キーワード 
トピック2:  人 口内 口 トラブル 環境 悪化 
トピック3:  チョコ バレンタイン 褒美 自分 ショコラ チョコレート 
-----8-----
子どもを薬嫌いにさせないための「服薬補助ゼリー」

トピック1:  子ども 薬 親 問題 ストレス 受験 
トピック2:  人 口内 口 トラブル 環境 悪化 
トピック3:  ヨガ ポーズ 人 犬 効果 下 
-----9-----
全身の健康は口から　口臭を「クマ笹歯みがき」で予防

トピック1:  人 口内 口 トラブル 環境 悪化 
トピック2:  紹介 方法 iphone 機能 今回 ダイエット 
トピック3:  チョコ バレンタイン 褒美 自分 ショコラ チョコレート 
-----10-----
胃腸薬「百草丸」が粘膜修復成分をプラスして新登場

トピック1:  将棋 愛 ガイド 登場 宴会 シーン 
トピック2:  紹介 方法 iphone 機能 今回 ダイエット 
トピック3:  人 口内 口 トラブル 環境 悪化 
-----11-----
ストレスからくる下痢…その原因と対処法は？

トピック1:  子ども 薬 親 問題 ストレス 受験 
トピック2:  人 口内 口 トラブル 環境 悪化 
トピック3:  塾 選び 受験 チェックポイント 中学生 失敗 
.
.
.
-----328-----
2016年は、こうして占いを使いこなす！

トピック1:  塾 選び 受験 チェックポイント 中学生 失敗 
トピック2:  ヨガ ポーズ 人 犬 効果 下 
トピック3:  トレンド 春 夏 ファッション 厳選 キーワード 
-----329-----
けっこう身近にある感動、東京23区内で見られる「絶景スポット」

トピック1:  紹介 今回 日本 月 金沢 五輪 
トピック2:  紹介 方法 iphone 機能 今回 ダイエット 
トピック3:  冬 雪見 露天風呂 温泉 紹介 季節 
-----330-----
2015D1グランプリ 「UP GARAGE」

トピック1:  対策 指輪 雪 女性 試験 男性 
トピック2:  子ども 薬 親 問題 ストレス 受験 
トピック3:  体 幹 トレーニング メニュー 基本 効果 
-----331-----
2015D1グランプリ 「GOOD YEAR」

トピック1:  紹介 今回 日本 月 金沢 五輪 
トピック2:  対策 指輪 雪 女性 試験 男性 
トピック3:  チョコ バレンタイン 褒美 自分 ショコラ チョコレート 
-----332-----
役所に社食……「え、ここ一般人も入っていいの？」なグルメスポット

トピック1:  紹介 今回 日本 月 金沢 五輪 
トピック2:  紹介 方法 iphone 機能 今回 ダイエット 
トピック3:  木 魅力 街 プロ 紹介 場所 
-----333-----
「2016DGRQ」はこの娘たち！

トピック1:  チョコ バレンタイン 褒美 自分 ショコラ チョコレート 
トピック2:  ヨガ ポーズ 人 犬 効果 下 
トピック3:  猫 目 映画 今回 理由 妊娠 
-----334-----
どこよりも美味いコロッケがある本郷菊坂でグルメ散歩

トピック1:  ヨガ ポーズ 人 犬 効果 下 
トピック2:  木 魅力 街 プロ 紹介 場所 
トピック3:  人 口内 口 トラブル 環境 悪化 
-----335-----
2016年「RAYBRIG レースクイーン」はこの娘たち！

トピック1:  紹介 今回 日本 月 金沢 五輪 
トピック2:  冬 雪見 露天風呂 温泉 紹介 季節 
トピック3:  塾 選び 受験 チェックポイント 中学生 失敗 
-----336-----
「東京オートサロン2016」コンパニオン速報第2弾

トピック1:  紹介 今回 日本 月 金沢 五輪 
トピック2:  紹介 方法 iphone 機能 今回 ダイエット 
トピック3:  チョコ バレンタイン 褒美 自分 ショコラ チョコレート 
-----337-----
「東京オートサロン2016」コンパニオン速報第1弾

トピック1:  紹介 今回 日本 月 金沢 五輪 
トピック2:  紹介 方法 iphone 機能 今回 ダイエット 
トピック3:  チョコ バレンタイン 褒美 自分 ショコラ チョコレート 
-----338-----
オムライスのある昔ながらの喫茶店を探して歩く

トピック1:  木 魅力 街 プロ 紹介 場所 
トピック2:  チョコ バレンタイン 褒美 自分 ショコラ チョコレート 
トピック3:  子ども 薬 親 問題 ストレス 受験 
-----339-----
ルーペで味わい尽くす！凹版切手の魅力

トピック1:  紹介 今回 日本 月 金沢 五輪 
トピック2:  ポイント 楽天 現金 方法 ネット スーパー 
トピック3:  住宅 建築 設計 事務所 経験 現在 
-----340-----
東京から日帰りで行ける、無料でも十分に楽しめる見学施設

トピック1:  人気 パン カフェ コーヒー 栃木 中古 
トピック2:  冬 雪見 露天風呂 温泉 紹介 季節 
トピック3:  紹介 今回 日本 月 金沢 五輪

全文書(340記事)について, 各文書の持つ潜在的なトピック上位3つを表示しました. なお, プログラムと同階層に結果を書き出したファイルarticle.txtが生成されます.

実際に, 340個目の文書「東京から日帰りで行ける、無料でも十分に楽しめる見学施設」を確認したところ, 抽出されたトピック通り, 「冬」に行って楽しめる「人気」の施設を「紹介」している記事でした. トピックをうまく抽出できているようです. 文書の持つ話題を的確に捉えていることが確認できました.

それではNMFの実装コードをまとめたファイルもGitHubにあげておきます.

まとめ

本記事ではトピックモデルの一種であるLSAを用いることによって, 多くのニュース記事から話題になっているトピックを抽出しました. また, 各文書が持つ潜在的な話題の抽出も行いました.

結果より, 文書が持つ話題を的確に抽出していることが確認できましたが, 「紹介」というトピックや, トピックにおいて出現確率の高い単語として「今回」「現在」のような副詞可能単語を確認しました. これらの単語は一般性が高いため, その文書を特徴づける単語としては適切ではありません. ゆえに, 文書の特徴の把握が難しくなります. したがって, 形態素解析によって形態素単位で分かち書きする処理の過程において, 「サ変接続」と「副詞可能」な単語も除外することによって, 把握が比較的容易なトピックの抽出が行えます.

補足

本記事では各トピックにおける出現確率の高い6個の単語の中で, 確率が最も高い単語をトピックであるかのように扱いましたが, 正しくはこの単語6個すべてが1つのトピック(話題のクラスタ)であり, そして話題クラスタごとに関連した単語が6個抽出されている状態です.

実際のところ, この話題クラスタが”何のトピック”であるかの決定は, 本人の裁量で行うができます. したがって, 本記事では話題クラスタの中で出現確率が最も高い単語をトピックとしました.
この辺りの話については, アイスクリーム屋さんで統計学がわかる -回帰分析・因子分析編- が分かりやすいので, 一読することをすすめます.

参考文献

• 岩田具治. “トピックモデル“. 2015.
• Toby Segaran. “集合知プログラミング“. 2008.

トピックモデルの基本についてはトピックモデルの4章を参考にしました. 実装には集合知プログラミングの10章を参考にしました.

最後に, トピックモデルについてまとめたスライド集(ALBERT Official Blog -『トピックモデルによる統計的潜在意味解析』読書会を開催中です)を見つけたのでリンクしておきます.

9月の下旬からつい1週間くらい前まで、テレビ朝日の総合ビジネス局でインターンシップをしていました。
そこで今回は、テレビ朝日のインターンシップについて自分の感想を交えながら説明したいと思います。これで来年多くの応募があれば幸いです。

インターンネット概要

インターンネットとは、現場で実際に行われているWebビジネスに携わることができるテレビ朝日のインターンシップで、今年が初めての試みのようです。自分が調べた限りでは、テレビ放送局が行うインターンで「テレビ×Web」の仕事を実際に経験させてくれるのはここしかないと思います。
また、このインターンなんと、賞金(予算)として1,000,000円が与えられます。これも他では無いでしょう。

まとめると、このインターンネットは、1,000,000円の予算でWebサービスを作る活動のことです。
なお、活動は2種類「現行サービスの改善策提案型」と「新規サービスの提案型」があります。応募するにあたってどちらに取り組むかまでは決める必要はありませんが、自分の中でこんなことがあったらオモシロイ、とか絶対これがあれば便利、と言ったアイデアをたくさん持って参加することをおすすめします。
また、応募はグループ応募と個人応募があります。個人で参加した場合は当日にグループを作ることができるので、問題ありません。ただし、あらかじめ自分の役割を明確にしておくことをおすすめします。

詳細

この活動の目的は、勝ち取った予算でWebサービスを作り、それを世に発信することです。0を1に、1を10に、全部自分の手で行うことができます。
したがって、活動は2段階に分かれます。1段目は予算を取る活動、2段目は提案サービスをカタチにする活動です。
前者は参加者全員取り組むことができますが、後者は勝ち取った者のみ取り組むことができます。

予算を取る活動

予算を取るためには、先進のスタッフの前でめっちゃくちゃ良いプレゼンをして、自分の提案を認めてもらう必要があります。
そのため、市場や現行サービスの問題点を含めた状況把握、どれくらいのお金が動くのかor得られそうかを含めたマネタイズ、そして解決策と言った材料が必要になります。
そこで本インターンでは、めっちゃくちゃ良いプレゼンをするために、材料を揃えるための方法論を教わります。
今回教わったのはデザインスプリントです。デザインスプリントの詳細は本記事では割愛しますが、簡単に説明すると、デザインスプリントは仮想の人間を作り、その人に提供する価値を考える方法です。

この活動ではデザインスプリントを通して得られた材料をスライドに反映して、それを発表します。
ここで提案が認められると、次のステップへ進むことができます。

提案サービスをカタチにする活動

ここからはメンター2, 3人の監督の下、提案サービスをカタチにしていきます。
活動スタイルですが、基本的には1ヶ月の間グループで自主的に作業し、週1日の頻度で行う局内でのメンターとの会合にて進捗を報告し、また問題点等の共有を行います。なお、状況によっては活動期間が変動する場合があります。
活動はグループで行いますが、基本的な作業は個々人の役割に沿って行います。

活動内容の詳細はまだ公開できませんが、ここで言えることは実に濃い内容の有意義な活動ができます。

まとめ

• 実業務に近い提案ができる
• • 提案をする相手・場はもちろんのこと、発表までの過程と提案が許可されてからそれをカタチにするまでの過程が実際の業務と非常に近いです。また、現場スタッフによるフィードバックを受けられます。
• メンターがつく
• • 先進の現場スタッフが綿密に指導してくれます。今回はSlackを用いることで密なコミュニケーションを図りました。おかげさまで問題を抱え込むことはほとんどありませんでした。
• 開発リソースを何でも使える
• • 予算があるため、開発にかかるリソースはほぼ使い放題です。したがって、データ解析, 機械学習等で計算機をガンガン回す作業もできます。
• 現場を見られる
• • 局内で現場スタッフの働く様子を見ることができます。また、話せる機会が多く存在します。
• Webビジネスの臨場感を味わえる
• • テレビ局が行うWebビジネスを話として聞ける場は多く存在しても、それを実際に経験できる場は恐らく他には存在しないでしょう。
• 開発ノウハウを知れる
• • 開発の回し方から運用の方法まで、実際に行われている開発のノウハウを多く教わることができました。

最後に

本インターンシップは、テレビ放送局の性質上、他業種・他職種の人と関わる機会が多く存在するため、多様な意見をもらいながらWebサービスを作ることができます。技術力はもちろん、考え方の成長も感じられることでしょう。

• Firefox Add-on のアドオンスクリプトから外部WebAPIをたたくには(クロスドメイン制約やらの問題を配慮して)XMLHTTPRequestではHTTP通信ができなくなっている.
• • XMLHTTPRequestがラッパされているAdd-on SDK提供のrequestモジュールを使えばHTTP通信ができる. 下記例.

1
2
3
4
5
6
7
8
9
10

var Request = require("sdk/request").Request;
var quijote = Request({
  url: "URL",
  overrideMimeType: "text/plain; charset=latin1",
  onComplete: function (response) {
    console.log(response.text);
  }
});

quijote.get();

– ちなみにレスポンスで受ける文字列が化けるのでcharsetはutf-8にするといい

• Widgetモジュールの使用は非推奨となっていた
• • uiモジュールを使うように
• モジュールのパス指定はsdk/から始めるように(省略すると実行時にwarningが出る)

下記はブラウザのメニューバーにアイコンを追加し, それをクリックすると新しいタブを開いてモジラのページへジャンプするコード

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

var buttons = require('sdk/ui/button/action');
var tabs = require("sdk/tabs");

var button = buttons.ActionButton({
  id: "mozilla-link",
  label: "Visit Mozilla",
  icon: {
    "16": "./icon-16.png",
    "32": "./icon-32.png",
    "64": "./icon-64.png"
  },
  onClick: handleClick
});

function handleClick(state) {
  tabs.open("https://www.mozilla.org/");
}