2016-10-05

Min HashによるJaccard係数の近似実験

概要

Jaccard係数は集合間の類似度を表す尺度(値域は0から1の間)であり, (1)式により定義されます(値が1に近づくほど類似度が高い).

$sim(C_i, C_j) = \frac{\mid C_i \cap C_j \mid}{\mid C_i \cup C_j \mid}$ ・・・(1)

一般に, (1)式はDBの中からクエリqとのJaccard係数が大きいデータ(集合)を探すような場合に, データ数nやデータの要素数dが大きいと計算時間($O(nd)$)が非常に大きくなる問題があります${}^{※1}$.
そこで今回は, 集合に対する確率的なハッシュ関数であるMin Hashを用いて, Jaccard係数を近似計算する実験を行ってみます. Min HashはJaccard係数に対するLocality Sensitive Hashingです.
※1 扱うデータはそれぞれ要素の種類数を次元とした2値ベクトル表現に変換しているとします.

Jaccard係数の性質

2つのベクトル$C_i = (1, 1, 0, 0)$, $C_j = (1, 0, 1, 0)$があるとします.

	タイプA	タイプB	タイプC	タイプD
$C_{i}$	1	1	0	0
$C_{j}$	1	0	1	0

このとき各列は値によって4種類に分類でき, タイプDはJaccard係数に関係ないので, $C_i$, $C_j$間の類似度は(2)式で表現できます.

$sim(C_i, C_j) = \frac{\mid A \mid}{\mid A \mid + \mid B \mid + \mid C \mid}$　・・・(2)

Min Hashの性質

Min Hashは, ベクトルの列入れ替え規則を持ったハッシュ関数mhをそれぞれのベクトルに適用した後, 最初に非ゼロが出現する位置(ハッシュ値)が一致する確率によってJaccard係数を近似する手法です. したがって, ベクトルの列をランダムに入れ替えたときにタイプA, B, Cのどれが最初に出現するかでハッシュ値が一致するかどうかが決まるため, 結局タイプDは関係なく, (3)式で表現されます.

$P[mh(C_i) = mh(C_j)] = \frac{\mid A \mid}{\mid A \mid + \mid B \mid + \mid C \mid}$　・・・(3)

なお, 実際にMin Hashを使うときはベクトルの列を入れ替えることはせずにランダムに生成したハッシュテーブル$r_{(t)}$を用意し, ハッシュテーブルを通してハッシュ値を求めます(データベースで列の入れ替えは処理が重いため).

例：$r_{(t)} = $ {$6, 1, 2, 3, 8, 7, 5, 4$}, $C_i = (1, 0, 0, 0, 1, 1, 1, 0)$のとき, $mh(C_i) = min${$6, 8, 7, 5$} $ = 5$

つまりMin Hashは作成したハッシュ関数(ハッシュテーブル$r_{(t)}$)をそれぞれの集合に適用した後に最小値を求め, それが一致する確率でJaccard係数を近似します. ハッシュ値が一致する確率は経験確率により近似計算します. 具体的には,

k個のハッシュ関数を用意し, $C_i$, $C_j$に対するk個のハッシュ値${}^{※2}$を得る
$C_i$, $C_j$のk個のハッシュ値のうち, いくつが一致するか数える
一致した数をkで割った確率がJaccard係数の近似値となる

kの数を増やせば増やすほど, 近似値はJaccard係数に近づきます.
※2 k個のハッシュ値はsketchとも呼ばれます.

重要な定理

ここで重要な定理は, $C_i$, $C_j$のハッシュ値が一致する確率はJaccard係数と等しいということです.

$P[mh(C_i) = mh(C_j)] = \frac{\mid C_i \cap C_j \mid}{\mid C_i \cup C_j \mid} = sim(C_i, C_j)$　・・・(4)

方針

DBの中からクエリの類似データを検索するタスクを用意します
Jaccard係数とMin Hashによる近似Jaccard係数を用いて類似データを検索します
Jaccard係数での検索結果を正解データとして, 近似Jaccard係数での検索結果でPrecision Recall Curveを作成します
kを増やすほどJaccard係数による検索結果に近づくのか, カーブの下がり具合を見て確かめます(カーブの右肩が座標(1, 1)に近いほど, Min Hashによる近似値はJaccard係数に近い)

方法

150個の集合をランダムに生成する
- 集合の要素種類数を400とし, 各要素を含むかどうかは確率的に決定する
集合の20%をクエリ, 80%をDBとする
クエリとのJaccard係数が大きい上位20個の集合を正解データとする
近似Jaccard係数による検索結果の上位100個について, Precision Recall Curveを作成する(ハッシュ値の数k = 100, 1000, 10000の場合について)
- $Precision = \frac{近似Jaccard係数による検索結果上位x個のうち正解データに入っているものの数}{検索結果件数x}$
- $Recall = \frac{近似Jaccard係数による検索結果上位x個のうち正解データに入っているものの数}{正解データ数}$
- 変数$x$は1~100

実装

Jaccard係数とMin Hashの実装

Jaccard係数とMin Hashを実装します. すべての集合を2値ベクトル表現にし, プログラムの実行時に引数でsketchの数kを指定できるようにしました.

# -*- coding: utf-8 -*-

from abc import ABCMeta, abstractmethod
import random
import sys
import math

class SimilarityCal(object):
    __metaclass__ = ABCMeta

    @abstractmethod
    def calculate(self, set_x, set_y):
        raise NotImplementedError("not implemented error.")
 
    # 重複要素のない集合の生成
    def uniqueSet(self, set_x, set_y):
        x = set(list(set_x))
        y = set(list(set_y))

        return x, y

    # 2値ベクトルの生成
    def binaryVector(self, set_x, set_y):
        # 集合の要素種類数
        set_xy =  set(list(set_x)) | set(list(set_y))

        x = []
        y = []
        
        for v in set_xy:
            if v in set_x:
                x.append(1)
            else:
                x.append(0)

            if v in set_y:
                y.append(1)
            else:
                y.append(0)

        return x, y

    # 1~引数lengthの範囲で重複なしの乱数を引数length分生成 (length = 集合の要素種類数)
    def generateRanNum(self, length):
        samples = random.sample(xrange(length + 1), length + 1)
        r_t = []

        for v in samples:
            if v != 0 and len(r_t) < length:
                r_t.append(v)

        return r_t


# Jaccard係数
class Jaccard(SimilarityCal):
    def calculate(self, set_x, set_y):
        x, y = self.uniqueSet(set_x, set_y)

        try:
            # 積集合/和集合
            result = float(len(x & y)) / len(x | y)
        except ZeroDivisionError:
            result = 0.0

        return result

# MinHash
class MinHash(SimilarityCal):
    def calculate(self, set_x, set_y):
        bagOfX, bagOfY = self.binaryVector(set_x, set_y)

        # 生成するMinHashの数
        k = int(sys.argv[1])
        # k個のハッシュ値のうち, いくつ一致したか
        counter = 0
        # 第一引数kの回数分ハッシュ関数を生成し, 比較する
        for i in xrange(k):
            hashX = []
            hashY = []

            # r(t)テーブルの生成
            r_t = self.generateRanNum(len(bagOfX))

            for i in xrange(len(bagOfX)):
                if bagOfX[i] == 1:
                    hashX.append(r_t[i])
            mh_x = min(hashX)

            for i in xrange(len(bagOfY)):
                if bagOfY[i] == 1:
                    hashY.append(r_t[i])
            mh_y = min(hashY)

            counter = counter + 1 if mh_x == mh_y else counter

        # MinHashを用いたJaccard係数の近似計算の結果を返す
        return float(counter) / k


if __name__ == '__main__':
    set_x = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 111, 555, 31, 49, 100, 1000, 1111, 111]
    set_y = [2, 3, 4, 6, 11, 22, 33, 44, 55, 111, 1111, 1000, 100, 10]
    print "MinHash", MinHash().calculate(set_x, set_y)
    print "Jaccard", Jaccard().calculate(set_x, set_y)

それではハッシュ値の数k = 5で実行してみます. なお, まとめたコードはGitHubにあげています.
1
2
3
$ python jaccard_minhash.py 5
MinHash 0.2
Jaccard 0.409090909091

次はk = 7で実行.

1
2
3

python jaccard_minhash.py 7
MinHash 0.571428571429
Jaccard 0.409090909091

k = 10で実行. kを増やすとMinHashによる近似Jaccard係数がJaccard係数に近づいていることが確認できます.
1
2
3
$ python jaccard_minhash.py 10
MinHash 0.4
Jaccard 0.409090909091

Precision Recall Curveを描画

データセットを生成します. 具体的には, 150個の集合をランダムに生成します. そして各集合の要素種類数を400とし, 各要素を含むかどうかは確率的に決定します. 用意したデータセットの20%をクエリ, 80%をDBとします.

# sketchの個数
kNum = 100
# 集合の個数
n = 150
# n個の集合
sets = []
# 要素の値域を[1, 400]つまり要素の種類数dを400にする
d = 400
# 集合の要素数を確率的に決める
prob = 0.3

# n個の集合を生成
for i in xrange(n):
    ary = [v for v in xrange(1, d + 1) if random.random() < prob]
    sets.append(ary)

# setsのうち20%をクエリ, 80%をDBにする
pivot = int(math.ceil(len(sets)*0.2))
query = sets[:pivot]
db = sets[pivot:]

Jaccard係数が大きい上位20個の集合を正解データとします.

# クエリとDBのJaccard係数を計算して値の昇順にソート
aryJaccard = []
for set_x in query:
    for set_y in db:
        dictJaccard = {}
        dictJaccard["Set"] = set_y
        dictJaccard["Score"] = Jaccard().calculate(set_x, set_y)
        aryJaccard.append(dictJaccard)
# 種類数 = query数 * db数
aryJaccard = sorted(aryJaccard, key = lambda x:x["Score"])

# Jaccard係数が大きい上位20件のDBを正解データとして使う
if len(aryJaccard) > 20:
    aryJaccard = aryJaccard[-20:]

kを100, 1000, 10000と変化させたときのPrecision Recall Curveを描画します. なお, PrecisionはInterpolated Precisionにしています.

plotDataSets_x = []
plotDataSets_y = []
plotDataSets_label = []

while kNum <= 10000:
    aryMinHash = []
    for set_x in query:
        for set_y in db:
            dictMinHash = {} 
            dictMinHash["Set"] = set_y
            dictMinHash["Score"] = MinHash().calculate(set_x, set_y, kNum)
            aryMinHash.append(dictMinHash)

    # 種類数 = query数 * db数
    aryMinHash = sorted(aryMinHash, key = lambda x:x["Score"])

    # MinHashによる近似Jaccard係数が大きい上位x(1~100)件
    plotData_x = []
    plotData_y = []
    for x in xrange(1, 101):
        MinHashResultStat = aryMinHash[-x:]

        # MinHashとJaccardの結果で一致する数をカウント
        counter = 0
        for dict_M in MinHashResultStat:
            MinHashResult = set(dict_M["Set"])
            countFlag = False
            for dict_J in aryJaccard:
                JaccardResult = set(dict_J["Set"])
                if len(MinHashResult) == len(JaccardResult):
                    counter = counter + 1 if len(MinHashResult & JaccardResult) == len(MinHashResult) else counter
                    countFlag = True
                if countFlag:
                    break
            if counter >= 20:
                break

        print x, ",",  kNum, ",", counter,  ",", (float(counter)/x), ",", (float(counter)/20)

        plotData_x.append(float(counter)/20)
        plotData_y.append(float(counter)/x)

    # interpolated precision
    for i in xrange(1, len(plotData_y)):
        if plotData_y[len(plotData_y)-i] > plotData_y[len(plotData_y)-(i+1)]:
            plotData_y[len(plotData_y)-(i+1)] = plotData_y[len(plotData_y)-i]

    plotDataSets_x.append(plotData_x)
    plotDataSets_y.append(plotData_y)
    plotDataSets_label.append("k="+str(kNum))

    kNum *= 10

# グラフ生成
fig = sns.mpl.pyplot.figure()
ax = fig.add_subplot(111)
for i in xrange(len(plotDataSets_label)):
    ax.plot(plotDataSets_x[i], plotDataSets_y[i], label=plotDataSets_label[i])

ax.legend()
sns.plt.title(u"Min HashによるJaccard係数の近似値を用いた類似検索結果のPrecision Recall Curve")
sns.plt.xlabel(u"Recall")
sns.plt.ylabel(u"Precision")
sns.plt.show()

実行結果です. まとめたコードはGitHubにあげています.

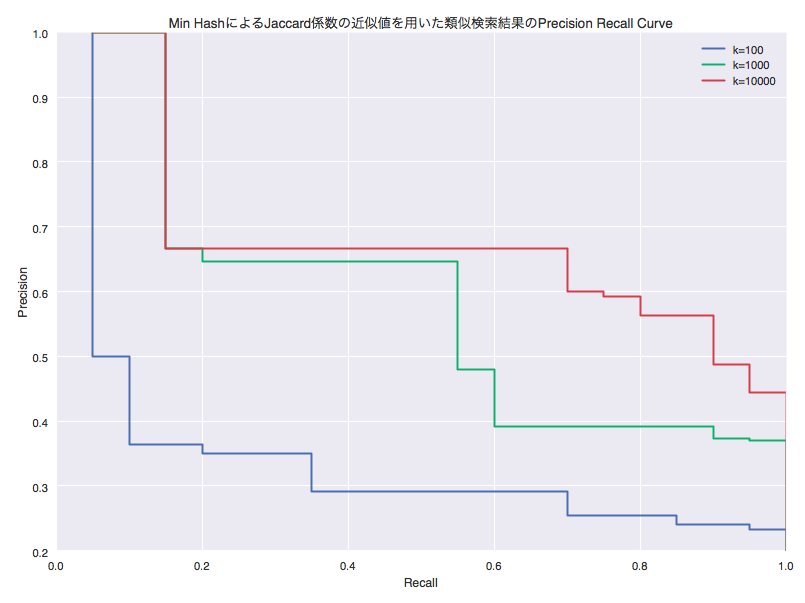
kを増やすほどカーブの右肩が座標(1, 1)に近づいていることが確認できます. 検索結果の精度が良くなっている(Min HashによるJaccard係数の近似値がJaccard係数に近づいている)ようです.

まとめ

本記事ではLocality Sensitive HashingであるMin Hashを用いて, Jaccard係数を近似する実験を行いました. 近似していることの確認は, Min Hashで生成するハッシュ値の数kを増やしていくことにより, 正解(Jaccard係数で導出したデータ)をどれだけ当てられるかを, Min Hashによる近似値についてのPredision Recall Curveを作成することで確かめました.

結果の図より, kを増やすとカーブの右肩が座標(1,1)に近づくため, Jaccard係数で導出した結果に近づいていくことを確認できました.

参考文献

“Jaccard係数とMin Hash“.
“Min Hashによる高速な類似検索“.

キャンベルとヨセミテ

Webまわりのいろいろなことを試してそれを公開してみるページ